Question

Given f(x)=(x-6)^2+7 find f^-1(x) then state whether f^-1(x) is a function

Answer 1

For this case we must find the inverse of the following function:

`f (x) = (x-6) ^ 2 + 7`

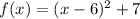
For this we follow the steps below:

Replace f (x) with y:

`y = (x-6) ^ 2 + 7`

We exchange the variables:

`x = (y-6) ^ 2 + 7`

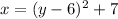
We solve the equation for "y", that is, we clear "y":

`(y-6) ^ 2 + 7 = x`

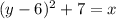
We subtract 7 on both sides of the equation:

`(y-6) ^ 2 = x-7`

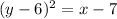
We apply square root on both sides of the equation to eliminate the exponent:

`y-6 = \sqrt {x-7}`

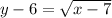
We add 6 to both sides of the equation:

`y = \pm \sqrt {x-7} +6`

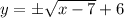
We change y by
`f ^ {- 1} (x):`

`f ^ {- 1} (x) = \pm \sqrt {x-7} +6`

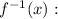
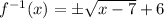
Answer;

`f ^ {- 1} (x) = \pm \sqrt {x-7} +6`

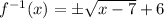
If it is a inverse function.