Question

Josiah claims that the ordered pair (6,-10) can be replaced with any ordered pair and the set will still represent a function. Select all ordered pairs that could be used to show that this claim is incorrect

Answer 1

Complete Question:

{(–9, 1), (–5, 2), (0, 7), (1, 3), (6, –10)} Josiah claims that the ordered pair (6, –10) can be replaced with any ordered pair and the set will still represent a function. Select all ordered pairs that could be used to show that this claim is incorrect.

A. (–10, –10)

B. (–9, –6)

C. (–5, 1)

D. (1, 12)

E. (4, 7)

Answer:

`B.\ (-9, -6)`

`C.\ (-5, 1)`

`D.\ (1, 12)`

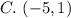
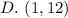
Explanation:

A relation is represented as:

`R->\{(x_1,y_1),(x_2,y_2),(x_3,y_3)...(x_n,y_n)\}`

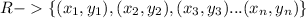
Where

`x = domain`

`y = range`

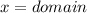
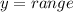
For a relation to be a function, the domain must be unique and must not be repeated.

In the given function,

`\{(-9, 1), (-5, 2), (0, 7), (1, 3), (6, -10)\}`

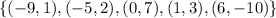
The domains are
`\{-9,-5,0,1,6\}`

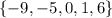
So, if (6,-10) is to be replaced;

The domain of the ordered pair that will replace it must not be any of
`\{-9,-5,0,1,6\}`

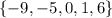
From the list of given options:

`B.\ (-9, -6)`

`C.\ (-5, 1)`

`D.\ (1, 12)`

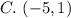
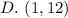
The above can not replace (6,-10) because their domain exist already.