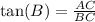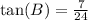Question

Find the exact values of the indicated trigonometric functions. Write fractions in lowest terms.

Find sin B and tan B.

Answer 1

`\text{sin}(B)=(7)/(25)`

`\text{tan}(B)=(7)/(24)`

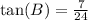
Explanation:

We have been given a right triangle. We are asked to find the
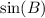`\text{sin}(B)` and
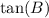`\text{tan}(B)` for our given triangle.

We know that sine relates opposite side of right triangle to its hypotenuse.

`\text{sin}=\frac{\text{Opposite}}{\text{Hypotenuse}}`

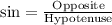
We can see that AC is opposite side to angle B and AB is hypotenuse of the given triangle.

`\text{sin}(B)=(AC)/(AB)`

`\text{sin}(B)=(7)/(25)`

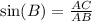
We know that tangent relates opposite side of right triangle to its adjacent.

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

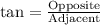
We can see that AC is opposite side to angle B and BC is adjacent side of the angle B.

`\text{tan}(B)=(AC)/(BC)`

`\text{tan}(B)=(7)/(24)`

Answer 2

For this case we have that by definition of trigonometric relations of a rectangular triangle, that the sine of an angle is given by the opposite leg to the angle on the hypotenuse of the triangle. While the tangent of the same angle is given by the leg opposite the angle on the leg adjacent to the angle.

Then, according to the figure we have:

`sin (B) = \frac {7} {25} = 0.28\\tg (B) = \frac {7} {24} = 0.2917`

Answer:

`sin (B) = \frac {7} {25}\\tg (B) = \frac {7} {24}`