Answer:
C
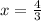
Explanation:
The given logarithmic equation is:
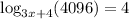
We rewrite in exponential form; to get;
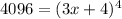
We rewrite the LHS as a certain natural number exponent 4.

The exponents are the same, hence the bases must also be the same.
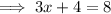
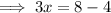
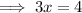
Divide both sides by 3;
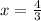
The correct answer is C