For this case we have:
Let k> 0:
To graph
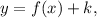 the graph k units is moved up.
the graph k units is moved up.
To graph
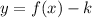 , the graph moves k units down.
, the graph moves k units down.
Let h> 0:
To graph
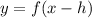 , the graph moves h units to the right.
, the graph moves h units to the right.
To graph
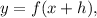 the graph moves h units to the left.
the graph moves h units to the left.
So, we have:
![y = f (x) = \sqrt [3] {x}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/tjp5zhfplff0ufc6g0sf0rzy6vtmo5jw7p.png)
Shifted 1 unit down and 4 to the left means:
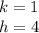
![y = f (x) = \sqrt [3] {x + 4} -1](https://img.qammunity.org/2020/formulas/mathematics/middle-school/spd2rb4ehasydav8qbghiq52sna9bl7rh1.png)
Answer:
Option D