Question

Need Help For This Question

Answer 1

The Answer is B

Explanation:

+7 at the end means up 7

The - 4 in the middle represents right 4

These are found using basic rules of translating equations

Answer 2

For this case we have to define function transformation that:

Let k> 0:

To graph
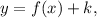`y = f (x) + k,` the graph is displayed k units up.

To graph
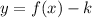`y = f (x) -k`, the graph is displayed k units units down.

Let h> 0:

To graph
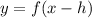`y = f (x-h)`, the graph moves units to the right.

To graph
`y = f (x + h)`, the graph moves h units to the left.

We have
`y = - \sqrt [3] {x}`

It moves 7 units up and 4 to the right.

So we have to:

`h = 4\\k = 7`

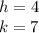
The shifted graphic is:

`y = - \sqrt [3] {x-4} +7`

ANswer:

`y = - \sqrt [3] {x-4} +7`