Since
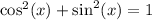
we have
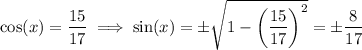
So, the first option is wrong. As for the tangent, we have
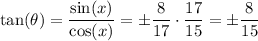
So, the second option is true, assuming that
 lies in the first quadrant.
lies in the first quadrant.
By definition, the secant is the inverse of the cosine, so the option is correct.
The cosecant is the inverse of the sine, so it should be +/- 15/8, and the option is incorrect.