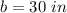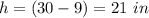Question

A hotel in Las Vegas, Nevada, is the largest pyramid in the United States. Prior to the construction of the building, the architects designed a scale model. The height of the scale model is 9 inches less than its length and its base is a square. If the volume of the model is 6300 cubic inches, write an equation describing the situation.

Answer 1

A is correct on edge 2022

Explanation:

Answer 2

The equation that describe the situation is

`b^(3)-9b^(2)-18,900=0`

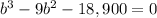
Explanation:

we know that

The volume of a square pyramid is equal to

`V=(1)/(3)b^(2) h`

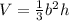
where

b is the length side of the square

h is the height of the pyramid

we have

`V=6,300\ in^(3)`

`h=(b-9)\ in`

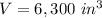
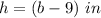
substitute the values and solve for b

`6,300=(1)/(3)b^(2) (b-9)\\ \\18,900=[b^(3)-9b^(2)]\\ \\b^(3)-9b^(2)-18,900=0`

Using a graphing calculator

`b=30\ in`

`h=(30-9)=21\ in`