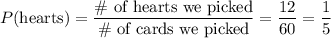Question

Suppose you select a card at random from a standard deck of cards 60 times, and 12 of those selections are hearts. How does the experimental probability compare to the theoretical probability? Include the difference between both types in your explanation.

Answer 1

A standard deck is composed of 52 cards, and contains 13 cards per suit. So, the theoretical probability of picking a card of any suit (and thus, in particular, a heart) is given by

`P(\text{hearts}) = \frac{\text{\# of hearts in the deck}}{\text{\# of cards in the deck}} = (13)/(52) = (1)/(4)`

On the other hand, the experimental probability is (as the name suggests) the probability that we can deduce from our experiment: we picked 60 cards, and 12 of these were hearts. This means that it would seem to us that

`P(\text{hearts}) = \frac{\text{\# of hearts we picked}}{\text{\# of cards we picked}} = (12)/(60) = (1)/(5)`