Answer:
No, the ladder will not be save at the height 16.5 feet from the ground
She must to buy 9 rolls to have enough crepe papers to decorate her ceiling
Explanation:
* Lets change the story problem to mathematics information
- The ladder , the wall and the ground formed together a right
angle triangle
- The wall and the ground are perpendicular to each other
- The length of the ladder is the hypotenuse of the triangle
- The vertical height of the ladder is the vertical leg of the triangle
- The horizontal distance between the ladder and the vertical wall
on the ground is the horizontal leg of the triangle
* Lets revise the trigonometry functions
- In any right angle triangle:
# The side opposite to the right angle is called the hypotenuse
# The other two sides are called the legs of the right angle
* If the name of the triangle is ABC, where B is the right angle
∴ The hypotenuse is AC
∴ AB and BC are the legs of the right angle
- ∠A and ∠C are two acute angles
- For angle A
# sin(A) = opposite/hypotenuse
∵ The opposite to ∠A is BC
∵ The hypotenuse is AC
∴ sin(A) = BC/AC
# cos(A) = adjacent/hypotenuse
∵ The adjacent to ∠A is AB
∵ The hypotenuse is AC
∴ cos(A) = AB/AC
# tan(A) = opposite/adjacent
∵ The opposite to ∠A is BC
∵ The adjacent to ∠A is AB
∴ tan(A) = BC/AB
* Lets solve the problem
- We need to calculate the measure of the angle between the
ladder and the ground, let it called Ф
- The vertical height is the opposite to this angle Ф
- The hypotenuse is the length of the ladder
∵ We have the opposite and the hypotenuse, we can use
the sin function
∵ sin(Ф) = opposite/hypotenuse
∵ The opposite is the vertical height = 16.5 feet
∵ The hypotenuse is the length of the ladder = 17 feet
∴ sin(Ф) = 16.5/17
∴ Ф =
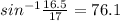 dgree
dgree
- The ladder will be save if the angle between the ladder and
the ground is no more than 70°
∵ The angle between the ladder and the ground is 76.1°
∴ Its measure is greater than 70°
* The ladder will not be save at the height 16.5 feet from the ground
* Lets study the information in the problem
- Katie wants to put the crepe paper around the perimeter of the
ceiling which shaped a square of side length 12 feet
- And also from each corner to the opposite corner
- She needs the length of the 4 sides of the square and the length
of its 2 diagonals
* Lets find the length of the diagonal of the square
∵ The two adjacent sides of the square formed two legs of a right
angle triangle and the diagonal joining the endpoints of the legs
is the hypotenuse of the triangle
- Use Pythagoras theorem to find the length of the diagonal
∴ The length of the diagonal = √(s² + s²) √(2s²) = s√2
∵ The length of the side of the square = 12 feet
∴ The length of the diagonal = 12√2
* Now lets find the length of the crepe papers she needs
∵ She needs the length of the 4 sides of the square and the length
of its 2 diagonals
∴ The length of crepe papers = 12 + 12 + 12 + 12 + 12√2 + 12√2 = 81.94 feet
∵ Each roll of the crepe papers contain 10 feet
- To find the number of rolls divide the length of the crepe papers by 10
∴ The number of rolls = 81.94 ÷ 10 = 8.194
* She must to buy 9 rolls to have enough crepe papers to decorate
her ceiling
* V.I.N:
- If she decide to buy 8 rolls, some part of ceiling will not decorate
because the 8 rolls have 80 feet only and she needs 81.94 feet