Question

What is
(3xy-1) (4xy+2)

Answer 1

12x^2y^2+2xy-2 with problems like these use the app “Photomath” it will help you a lot.

Answer 2

Hello!

The answer is:

`(3xy-1)(4xy+2)=12(xy)^(2)+2xy-2`

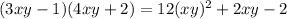
or

`(3xy-1)(4xy+2)=12x^(2)y^(2)+2xy-2`

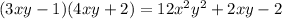
Why?

To solve the problem and identify the resultant expression, we need to apply the distributive property, and the, add or subtract like terms.

Describing the distributive property:

`(a+b)(c+d)=a*c+a*d+b*c+b*d`

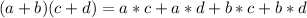
Remember, like terms are the terms that share the same variable and same exponent, for example:

`a^(2) +3a^(2)+a^(3)=4a^(2)+a^(3)`

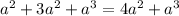
We were able to add only the terms that have the same exponent (2).

We are given the expression:

`(3xy-1)(4xy+2)`

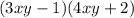
Now, solving we have:

`(3xy-1)(4xy+2)=(3xy*4xy)+(3xy*2)-(1*4xy)-2\\\\(3xy*4xy)+(3xy*2)-(1*4xy)-2=12(xy)^(2)+6xy-4xy-2\\\\12(xy)^(2)+6xy-4xy-2=12(xy)^(2)+2xy-2`

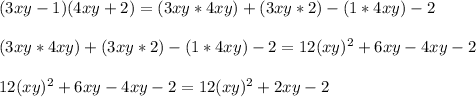
Hence, we have that:

`(3xy-1)(4xy+2)=12(xy)^(2)+2xy-2`

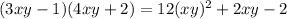
or

`(3xy-1)(4xy+2)=12x^(2)y^(2)+2xy-2`

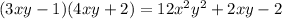
Have a nice day!