Hello!
The answer is:
The second option,
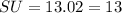
Why?
We are working with a right triangle, it means that we can use the following trigonometric property:
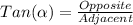
Which applied to our problem, will be:

We are given:
m∠S, equal to 21°
The side TU (opposite) equal to 5 units.
So, substituting and calculating we have:
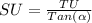
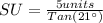
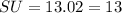
Hence, the answer is the second option
Have a nice day!