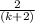Question

Look at my question

Answer 1

option D

`(2)/((k+2))`

Step-by-step explanation:

Given in the question an expression

`(4k+2)/(k^(2)-4).(k-2)/(2k+1)`

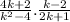
Step 1

Use Algebraic Formula

a² - b² = (a-b)(a+b)

k² - 4 = k² - (2)² = (k-2)(k+2)

`(4k+2)/((k-2)(k+2)).(k-2)/(2k+1)`

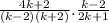
Step 2

Cancel(k-2) from both numerator and denometor

`(4k+2)/((k+2)).(1)/(2k+1)`

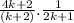
Step 3

Use Distributive Law

a(b+c) = (ab + ac)

4k + 2 = 2(2k+1)

`(2(2k+1))/((k+2)).(1)/(2k+1)`

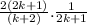
Step 4

Cancel(2k+1) from both numerator and denometor

`(2)/((k+2)).(1)/(1)`

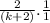
Step 5

Simplified form is

`(2)/((k+2))`