Question

asked Sep 12, 2020 142k views

1 Answer

DDovzhenko · Answer 1 · 2020-09-15T21:22:17+0000

Hello!

The answer is:

The second option,

$(\sqrt[m]{x^(a) } )^(b)=\sqrt[m]{x^(ab) }$

Discarding each given option in order to find the correct one, we have:

$\sqrt[m]{x}\sqrt[m]{y}=\sqrt[2m]{xy}$

The statement is false, the correct form of the statement (according to the property of roots) is:

$\sqrt[m]{x}\sqrt[m]{y}=\sqrt[m]{xy}$

$(\sqrt[m]{x^(a) } )^(b)=\sqrt[m]{x^(ab) }$

The statement is true, we can prove it by using the following properties of exponents:

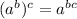
(a^(b))^(c)=a^(bc)

$\sqrt[n]{x^(m) }=x^{(m)/(n) }$

We are given the expression:

$(\sqrt[m]{x^(a) } )^(b)$

So, applying the properties, we have:

$(\sqrt[m]{x^(a) } )^(b)=(x^{(a)/(m)})^(b)=x^{(ab)/(m)}\\\\x^{(ab)/(m)}=\sqrt[m]{x^(ab) }$

Hence,

$(\sqrt[m]{x^(a) } )^(b)=\sqrt[m]{x^(ab) }$

$a\sqrt[n]{x}+b\sqrt[n]{x}=ab\sqrt[n]{x}$

The statement is false, the correct form of the statement (according to the property of roots) is:

$a\sqrt[n]{x}+b\sqrt[n]{x}=(a+b)\sqrt[n]{x}$

$\frac{\sqrt[m]{x} }{\sqrt[m]{y}}=m√(xy)$

The statement is false, the correct form of the statement (according to the property of roots) is:

$\frac{\sqrt[m]{x} }{\sqrt[m]{y}}=\sqrt[m]{(x)/(y) }$

Hence, the answer is, the statement that is true is the second statement:

$(\sqrt[m]{x^(a) } )^(b)=\sqrt[m]{x^(ab) }$

Have a nice day!