Answer:
The factorization of
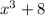 is
is

Explanation:
The problem is a sum of cubes factorization, this type of factorization applies only in binomials of the form
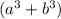 which means numbers that have exact cubic root and the exponents of the letters a and b are multiples of three.
which means numbers that have exact cubic root and the exponents of the letters a and b are multiples of three.
Sum of cubes equation

So, let's factor
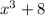
we have to bring the equation to the form
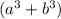
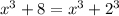 con
con
 y
y
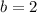
Solving using sum of cubes equation
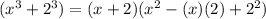

.