Question

Which equation represents the graph?

A) y=[x] + 2.5

B) y=[x] -2.5

C) y=[x -2.5]

D) y=[x + 2.5]​

Answer 1

y= |x|-2.5

Explanation:

The attached picture is the graph for the function y=|x|

The picture you asked differs in the origin of the graph, which resides in the point (0, -2.5).

So our equation should look like the following

y=a|x|+b

From the first point you have (0, -2.5), This means 0=a*|0|+b, we have obtained that b=-2.5

Now 'a' is the slope, we need to find another point in the graph. that would be (2.5, 0) (obtained from the given graph)

the slope is obtained using the equation

`a=(x_(2)-x_(1) )/(y_(2)-y_(1)  )`

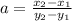
Where (x1, y1)= (0, -2.5), (x2,y2)=(2.5,0)

thus we have that a=1

So our equation is y=|x|-2.5