Question

SOMEONE PLEASE HELP ME

Answer 1

You can use a graphing calculator (Desmos for an example) to solve 36. And you would multiply 2x+3 • 4x+5 to find the area by the foil/distribution method (2x+3)(4x*5)

Answer 2

Question 1:

For this case we must indicate the graph corresponding to:

`y = x ^ 2 + 6x + 9`

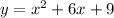
We factor the expression by looking for two numbers that multiplied give as a result 9 and added as a result 6. These numbers are 3 and 3:

`3 + 3 = 6\\3 * 3 = 9`

So:

`y = (x + 3) (x + 3) = (x + 3) ^ 2`

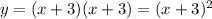
We use the form of vertex of a parabola:

`y = a (x-h) ^ 2 + k\\y = (x + 3) ^ 2`

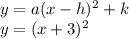
So:

a = 1

h = -3, is moved 3 units to the left

k = 0

The vertex of the parabola is given by:
`(h, k) = (- 3,0)`

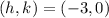
Since
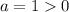`a = 1> 0` then the parabola is concave upwards.

With these data we can conclude that the correct option is the option H.

Answer:

Option H

Question 2:

For this case we have by definition, that the area of a rectangle is given by:

`A = a * b`

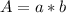
Where a and b are the sides of the rectangle.

We have as data that:

`a = 4x + 5\\b = 2x + 3`

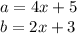
Then, the area is given by:

`A = (4x + 5) (2x + 3)`

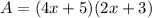
We must apply distributive property, which by definition establishes that:

`(a + b) (c + d) = ac + ad + bc + bd`

Then the area of the rectangle is given by:

`A = 8x ^ 2 + 12x + 10x + 15\\A = 8x ^ 2 + 22x + 15`

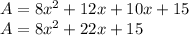
Answer:

Option D