Answer:
The factorization of
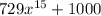 is
is
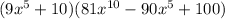
Explanation:
This is a case of factorization by sum and difference of cubes, this type of factorization applies only in binomials of the form
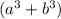 or
or
 . It is easy to recognize because the coefficients of the terms are perfect cube numbers (which means numbers that have exact cubic root, such as 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, etc.) and the exponents of the letters a and b are multiples of three (such as 3, 6, 9, 12, 15, 18, etc.).
. It is easy to recognize because the coefficients of the terms are perfect cube numbers (which means numbers that have exact cubic root, such as 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, etc.) and the exponents of the letters a and b are multiples of three (such as 3, 6, 9, 12, 15, 18, etc.).
Let's solve the factorization of
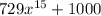 by using the sum and difference of cubes factorization.
by using the sum and difference of cubes factorization.
1.) We calculate the cubic root of each term in the equation
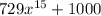 , and the exponent of the letter x is divided by 3.
, and the exponent of the letter x is divided by 3.
![\sqrt[3]{729x^(15)} =9x^(5)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/f6nx29qyi9p1ovu11ijz9d8qivy89v5d9s.png)
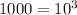 then
then
![\sqrt[3]{10^(3)} =10](https://img.qammunity.org/2020/formulas/mathematics/middle-school/z17lvxnjtjdsl77v26oiesemy5geybw035.png)
So, we got that
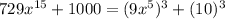 which has the form of
which has the form of
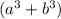 which means is a sum of cubes.
which means is a sum of cubes.
Sum of cubes
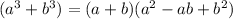
with
 y
y
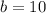
2.) Solving the sum of cubes.
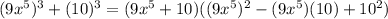
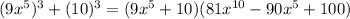
.