Hello!
The answer is:
The sixth option,
[-6,6]
Why?
To solve the problem, we need to find which of the given options match with the solution to the inequality. As we know, solving inequalities is almost the same that solving equalities, we need to isolate the variable and then, find where it satisfies the given condition (inequality)
So, solving the inequality we have:
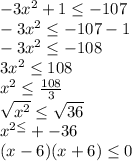
Therefore, we have that the solutions to the inequality are:
First solution:

Second solution:
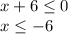
Hence, the correct option is the sixth option, the solution is described by the following solution set :
[-6,6]
Have a nice day!