Question

A plane is flying east at 115 m/s. The wind accelerates it at 2.88 m/s^2 directly northwest. After 25.0s, what is the magnitude of the velocity of the plane?

Answer 1

81.8 m/s

Step-by-step explanation:

The initial velocity of the plane is:

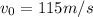`v_0=115 m/s` (toward east)

So, decomposing along the x- and y- directions:

`v_(x0) = 115 m/s\\v_(y0) = 0`

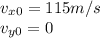
(we took east as positive x-direction and north as positive y-direction)

The acceleration is

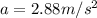`a=2.88 m/s^2` (northwest, so the angle with the positive x-direction is 135 degrees)

Decomposing it along the two directions:

`a_x = a cos 135^(\circ) = (2.88 m/s^2)(cos 135^(\circ))=-2.04 m/s^2\\a_y = a sin 135^(\circ) = (2.88 m/s^2)(sin 135^(\circ))=2.04 m/s^2`

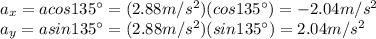
So the two components of the velocity after a time t = 25.0 s will be

`v_x = v_(x0) + a_x t = 115 m/s + (-2.04 m/s^2)(25.0 s)=64 m/s\\v_y = v_(y0) + a_y t = 0 m/s + (2.04 m/s^2)(25.0 s)=51 m/s`

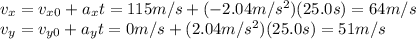
So, the magnitude of the velocity of the plane will be

`v=\sqrt[v_x^2+v_y^2}=√((64 m/s)^2+(51 m/s)^2)=81.8 m/s`