Question

Find the surface area of the following figure

Answer 1

510.4 ft²

Explanation:

We have:

two trapezoids with bases 15ft and 7ft and height 5ft.

four rectangles 5ft × 11ft, 15ft × 11ft, 9.4ft × 11ft and 7ft × 11ft.

The formula of an area of a trapezoid:

`A_t=(b_1+b_2)/(2)\cdot h`

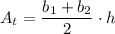
b₁, b₂ - bases

h - height

Substitute:

`A_t=(15+7)/(2)\cdot5=(22)/(2)\cdot5=(11)(5)=55\ ft^2`

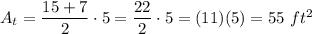
The formula of an area of a rectangle:

`A_r=lw`

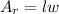
l - length

w - width

The dimensions of rectangle l × w

Subtitute:

`A_1=(5)(11)=55\ ft^2\\\\A_2=(15)(11)=165\ ft^2\\\\A_3=(9.4)(11)=103.4\ ft^2\\\\A_4=(7)(11)=77\ ft^2`

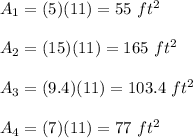
The surface area of the figure:

[tex]S.A.=2A_t+A_1+A_2+A_3+A_4\\\\S.A.=2(55)+55+165+103.4+77=510.4\ ft^2[/text]