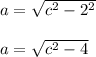Question

The Pythagorean Theorem says that in a right triangle, a2 + b2 = c2 , where a and b are the lengths of the legs, and c is the length of the hypotenuse. If b = 2, what is the length of side a in terms of c? Remember, “in terms of c” means that the variable c will appear in your answer.

Answer 1

Final answer is
`a=√(c^2-4)`.

Explanation:

Given that b=2. Now using Pythagorean theorem, we need to find the value of a in terms of c.

So let's plug b=2 into formula :

`a^2+b^2=c^2`

`a^2+2^2=c^2`

`a^2+4=c^2`

`a^2=c^2-4`

Take square root of both sides and use principle root as side length can't be negative.

`a=√(c^2-4)`

Hence final answer is
`a=√(c^2-4)`.

Answer 2

Answer:
`a=√(c^2-4)`

Explanation:

You know that the Pythagorean Theorem is:

`a^2+b^2=c^2`

Where "a" and "b" are the legs and "c" is the hypotenuse.

Then, since you need to find the length of side "a" in terms of the hypotenuse "c", you need to solve for "a":

Subtract b² from both sides of the equation:

`a^2+b^2-b^2=c^2-b^2`

`a^2=c^2-b^2`

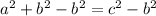
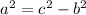
And finally, you need to apply square root to both sides of the equation:

`√(a^2)=√(c^2-b^2)\\\\a=√(c^2-b^2)`

Then:

`a=√(c^2-2^2)\\\\a=√(c^2-4)`