Question

A 120 kg Santa Claus slides down a 9 m chimney. He drops from his sleigh 2 m above the top of the chimney. It’s a tight fit, but he slides the whole way. He just comes to rest as he reaches the hearth. What is the force of friction on Santa from the chimney?A) 750 NB) 2000 NC) 2500 ND) 3200 NE) 1500 N

Answer 1

E) 1500 N

Step-by-step explanation:

The total height from which Santa has fallen down is

h = 9 m + 2 m = 11 m

So its gravitational potential energy at the beginning was

`U=mgh=(120 kg)(9.81 m/s^2)(11 m)=12,949 J`

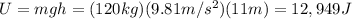
While sliding down, Santa has lost all its gravitational potential energy: this energy has been converted into thermal energy due to the presence of the friction. So, the work done by friction is exactly equal to the initial potential energy of Santa:

`W=12,949 J`

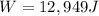
The work done by friction is

`W=Fd`

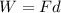
where

F is the force of friction

d = 9 m is the length of the chimney (the distance through which the frictional force acts)

Solving the equation for F, we find

`F=(W)/(d)=(12,949 J)/(9 m)=1439 N`

So the closest option is

E) 1500 N