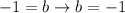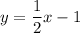Question

Plz answer both for me plz

Answer 1

`\large\boxed{\text{Table 1:}\ y=4x+1}\\\boxed{\text{Table 2:}\ y=(1)/(2)x-1}`

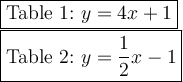
Explanation:

Tables show linear functions.

The slope-intercept form of an equation of a line:

`y=mx+b`

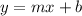
m - slope

b - y-intercept → (0, b)

The formula of a slope:

`m=(y_2-y_1)/(x_2-x_1)`

===================================================

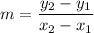
Table 1:

(0, 1) → b = 1, (1, 5)

`m=(5-1)/(1-0)=(4)/(1)=4\\\\y=4x+1`

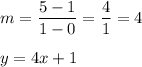
Table 2:

(4, 1), (6, 2)

`m=(2-1)/(6-4)=(1)/(2)\\\\y=(1)/(2)x+b`

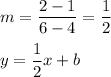
Put the coordinateso f the point (4, 1) to the equation of a line:

`1=(1)/(2)(4)+b`

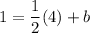
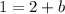`1=2+b` subtract 2 from both sides

`-1=b\to b=-1`

`y=(1)/(2)x-1`