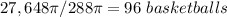Question

A cylindrical shaped drum is used to store basketballs in a gymnasium. The hollow drum measures 48 inches high with a 24 inch radius. If the radius of a basketball is 6 inches, the maximum number of basketballs that the cylindrical drum contains is ______ (192, 48, 96)

Answer 1

`96\ basketballs`

Explanation:

step 1

Find the volume of the cylinder (hollow drum)

The volume is equal to

`V=\pi r^(2) h`

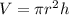
we have

`h=48\ in`

`r=24\ in`

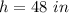
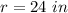
substitute

`V=\pi (24)^(2) (48)`

`V=27,648\pi\ in^(3)`

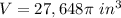
step 2

Find the volume of one basketball

The volume of the sphere is equal to

`V=(4)/(3)\pi r^(3)`

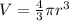
we have

`r=6\ in`

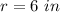
substitute

`V=(4)/(3)\pi (6)^(3)`

`V=288\pi\ in^(3)`

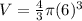
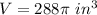
step 3

Find the maximum number of basketballs that the cylindrical drum contains

so

Divide the volume of the cylinder by the volume of one basketball

`27,648\pi/288\pi=96\ basketballs`