Final Answer:
The proposed new cereal box design has dimensions of 6 inches in length, 2 inches in width, and 8 inches in height. This design maintains the original cereal volume of 96 cubic inches while reducing the surface area to 104 square inches.
Step-by-step explanation:
The formula for the surface area
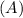 of a rectangular prism is given by:
of a rectangular prism is given by:
![\[ A = 2lw + 2lh + 2wh \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ccqju6hu4ahvz4jm216tecg4ts240odn94.png)
For the original box with dimensions 8 inches in length
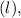 1 inch in width
1 inch in width
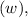 and 12 inches in height
and 12 inches in height
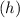 :
:
![\[ A_{\text{original}} = 2(8 * 1) + 2(8 * 12) + 2(1 * 12) = 232 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/74yc6ghfiagrkelasjz8qtyqd8ngrl1umo.png)
For the proposed new design with dimensions 6 inches in length, 2 inches in width, and 8 inches in height:
![\[ A_{\text{new}} = 2(6 * 2) + 2(6 * 8) + 2(2 * 8) = 104 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/gs0lozj5wg2wgbus9d3ljugqkpp7ee1bwl.png)
Comparing the surface areas, the new design significantly reduces it from 232 square inches to 104 square inches. This reduction in surface area indicates that the proposed design will require less material for manufacturing.
By maintaining the original cereal volume of 96 cubic inches while decreasing the surface area, the proposed cereal box design is more cost-effective to manufacture. The optimization of dimensions ensures that the same cereal quantity can be accommodated with a reduction in manufacturing costs.