Question

if you have 10 grams of a substance that decays with a half life of 14 days then how much will you have after 70 days?

Answer 1

Answer: If it has a 1/2 life of 14 days, after 14 days there will be half of it left correct?

Explanation:So, how many half-lifes are in 42 days?

42 / 14 = 3

This means it will divide 3 times.

1st half life period: 10 / 2 = 5g

2nd period: 5 / 2 = 2.5g

3rd period: 2.5 / 2 = 1.25g

10 g at start, 5 g at 14 days, 2.5 g at 28 days, 1.25 g at 42 days.

Answer 2

Answer: The amount of substance left will be 0.316 grams.

Step-by-step explanation:

All the decay processes follow first order kinetics.

The equation used to calculate half life for first order kinetics:

`t_(1/2)=(0.693)/(k)`

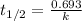
where,

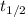`t_(1/2)` = half life of the reaction = 14 days

k = ?

Putting values in above equation, we get:

`k=(0.693)/(14days)=0.0495days^(-1)`

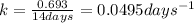
Rate law expression for first order kinetics is given by the equation:

`t=(2.303)/(k)\log(a)/(y)`

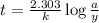
where,

k = rate constant =
`0.0495days^(-1)`

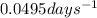
t = time taken for decay process = 70 days

a = initial amount of the reactant = 10 grams

y = amount left after decay process = ? grams

Putting values in above equation, we get:

`70days=(2.303)/(0.0495days^(-1))\log(10g)/(y)\\\\y=0.316g`

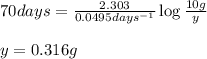
Hence, the amount of substance left will be 0.316 grams.