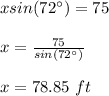Question

The wind has blown a tree so that it is growing at a 108° angle with the ground. The top of the tree is 75 ft. from the ground. How tall is the tree?

Answer 1

Answer: 78.85 ft

Explanation:

Based on the information provided in the exercise, you can draw the right triangle attached, wheree "x" is the height of the tree.

You need to remember the following identity:

`sin\alpha=(opposite)/(hypotenuse)`

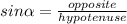
By definition:

`\alpha+108\°=180\°`

Then, this is:

`\alpha=180\°-108\°\\\alpha =72\°`

In the right triangle shown in the figure, you can identify:

`opposite=75\\hypotenuse=x`

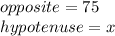
Then, you need to substitute the corresponding values into
`sin\alpha=(opposite)/(hypotenuse)`:

`sin(72\°)=(75)/(x)`

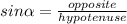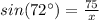
Now, you can solve for "x":

`xsin(72\°)=75\\\\x=(75)/(sin(72\°))\\\\x=78.85\ ft`