Answer:
The solutions are:
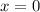 and
and
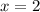 and
and

Explanation:
1) Make the function equal to zero
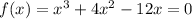
2) Take x as a common factor
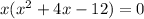
3) Factor the expression
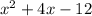
The sought-after factors are such numbers that when multiplying them obtain as result -12 and when adding both numbers obtain as result 4.
The numbers that meet this condition are
6 and -2
Because
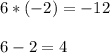
Then the factors are
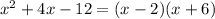
4) Solve the equation for x
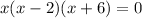
The solutions are:
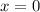 and
and
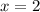 and
and
