Question

The base of a tower with the height of 55 meters is the 37 meters from point A . Find the angle of elevation from point A to the top of the tower .

Answer 1

Answer:47. 72°

Explanation:

from the attached figure below; adjacent =37 hypotenuse=55

θ = ?

From trig. formular,

cos θ = adjacent / hypotenuse

cos θ = 37 / 55

cos θ =0. 6727

θ = cos⁻¹ (0. 6727)

θ = 47. 72°

The angle of elavation is 47. 72°

Answer 2

56.07 degrees

Explanation:

This is a classic problem involving right triangle trig. We are looking for the angle that has a side opposite it with a measure of 55 m and a side adjacent to it with a measure of 37 m. This is the tangent ratio of the missing angle. Our equation then looks like this:

`tan\theta=(55)/(37)`

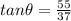
To find a missing angle on your calculator in degree mode, hit 2nd then tan and you'll see "tan^-1( " on your display. After the open parenthesis, enter your fraction and hit the enter button to get the angle measure. 56.07°