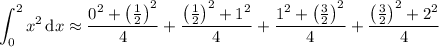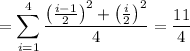Question

Using 4 equal-width intervals, show that the trapezoidal rule is the average of the upper and lower sum estimates for the integral from 0 to 2 of x squared, dx .

Answer 1

Split up the interval [0, 2] into 4 subintervals, so that

`[0,2]=\left[0,\frac12\right]\cup\left[\frac12,1\right]\cup\left[1,\frac32\right]\cup\left[\frac32,2\right]`

Each subinterval has width
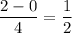`\frac{2-0}4=\frac12`. The area of the trapezoid constructed on each subinterval is
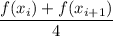`\frac{f(x_i)+f(x_(i+1))}4`, i.e. the average of the values of
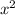`x^2` at both endpoints of the subinterval times 1/2 over each subinterval
`[x_i,x_(i+1)]`.

So,

`\displaystyle\int_0^2x^2\,\mathrm dx\approx\frac{0^2+\left(\frac12\right)^2}4+\frac{\left(\frac12\right)^2+1^2}4+\frac{1^2+\left(\frac32\right)^2}4+\frac{\left(\frac32\right)^2+2^2}4`

`=\displaystyle\sum_(i=1)^4\frac{\left(\frac{i-1}2\right)^2+\left(\frac i2\right)^2}4=\frac{11}4`