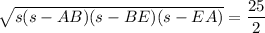Question

Geometry Question attached below

Answer 1

I'm sure there's an easier way to do this, but this method does work:

First, AB = CD = CG + GF + FD, so FG = 2.

By the Pythagorean theorem, in triangle AFD we get

`1^2+3^2=A F^2\implies A F=√(10)`

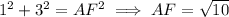
and in triangle BCG,

`2^2+3^2=BG^2\implies BG=√(13)`

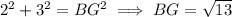
Angles AFD and EFG form a vertical pair, so they are congruent and have measure

`m\angle EFG=\tan^(-1)3`

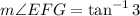
Similarly, angles BGC and FGE are congruent and have measure

`m\angle FGE=\tan^(-1)\frac32`

Then the remaining angle in triangle EFG has measure

`m\angle FEG=\pi-\tan^(-1)3-\tan^(-1)\frac32`

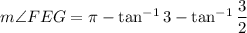
We can solve for the lengths of FE and GE exactly by applying the law of sines:

`\frac{\sin\left(\pi-\tan^(-1)3-\tan^(-1)\frac 32\right)}2=(\sin\left(\tan^(-1)3\right))/(GE)=(\sin\left(\tan^(-1)\frac32\right))/(FE)`

`\implies GE=\frac{2√(13)}3,FE=\frac{2√(10)}3`

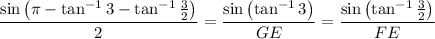
Let
`s` be the semiperimeter of triangle ABE, so that

`s=\frac{AB+BE+EA}2`

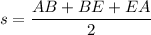
Then according to Heron's formula, the area of triangle ABE is

`√(s(s-AB)(s-BE)(s-EA))=\frac{25}2`