Answer:
By comparing both the payments we can say that Dealer A is cheaper by $4.50.
Explanation:
Dealership A: The car costs $30,000, and the loan has an annual interest rate of 4.8% for 5 years.
The EMI formula is :

Now, p = 30000
r =
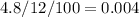
n =
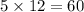
Putting values in formula we get;
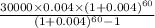
=>
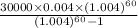
EMI is = $563.34
Dealership B: The car costs $29,800, and the loan has an annual interest rate of 5.4% for 5 years.
p = 29800
r =

n =
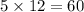
Putting values in formula we get;
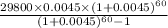
=>
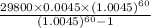
EMI = $567.84
By comparing both the payments we can say that Dealer A is cheaper by $4.50.