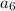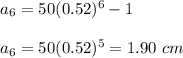Answer:
a)
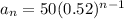
b)
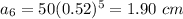
Explanation:
If each curved path has 52% of the previous height this means that
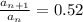
Then the radius of convergence is 0.52 and this is a geometric series.
The geometric series have the form:

Where
 is the first term of the series and r is the radius of convergence.
is the first term of the series and r is the radius of convergence.
In this problem
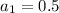 meters = 50 cm
meters = 50 cm
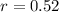
a) Then the rule for the sequence is:
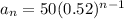
b) we must calculate