Question

Sketch the graph of y=2(x-2)2+5 and identify the axis of symmetry.

Answer 1

x=2

Explanation:

Answer 2

See attachment.

EXPLANATION

The given function is

`y = 2 {(x - 2)}^(2) + 5`

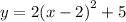
This equation is of the form:

`y = a {(x - h)}^(2) + k`

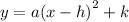
where (h,k) is the vertex of the parabola and

`x = h`

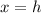
is the equation of axis of symmetry.

By comparing, h=2 and k=5, a=2

Hence the vertex is at (2,5).

and the equation of axis of symmetry is

`x = 2`

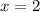
Since the value of 'a' is positive, the graph is a minimum graph.

With these information we can sketch the graph easily.

See attachment.