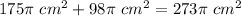Question

Find the volume and surface area of the composite figure. Give your answer in terms of π. HELP ASAP!!

Answer 1

Part 1) The volume of the composite figure is
`620.7\pi\cm^(3)`

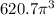
Part 2) The surface area of the composite figure is
`273\pi\ cm^(2)`

`V=620.7\pi\cm^(3), S=273\pi\ cm^(2)`

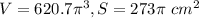
Explanation:

Part 1) Find the volume of the composite figure

we know that

The volume of the figure is equal to the volume of a cone plus the volume of a hemisphere

Find the volume of the cone

The volume of the cone is equal to

`V=(1)/(3) \pi r^(2) h`

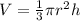
we have

`r=7\ cm`

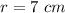
Applying Pythagoras Theorem find the value of h

`h^(2)=25^(2) -7^(2) \\ \\h^(2)= 576\\ \\h=24\ cm`

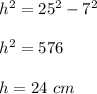
substitute

`V=(1)/(3) \pi (7)^(2) (24)`

`V=392 \pi\cm^(3)`

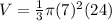
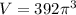
Find the volume of the hemisphere

The volume of the hemisphere is equal to

`V=(4)/(6)\pi r^(3)`

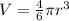
we have

`r=7\ cm`

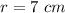
substitute

`V=(4)/(6)\pi (7)^(3)`

`V=228.7\pi\cm^(3)`

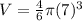
therefore

The volume of the composite figure is equal to

`392 \pi\cm^(3)+228.7\pi\cm^(3)=620.7\pi\cm^(3)`

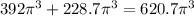
Part 2) Find the surface area of the composite figure

we know that

The surface area of the composite figure is equal to the lateral area of the cone plus the surface area of the hemisphere

Find the lateral area of the cone

The lateral area of the cone is equal to

`LA=\pi rl`

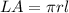
we have

`r=7\ cm`

`l=25\ cm`

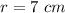
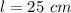
substitute

`LA=\pi(7)(25)`

`LA=175\pi\ cm^(2)`

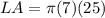
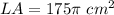
Find the surface area of the hemisphere

The surface area of the hemisphere is equal to

`SA=2\pi r^(2)`

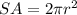
we have

`r=7\ cm`

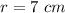
substitute

`SA=2\pi (7)^(2)`

`SA=98\pi\ cm^(2)`

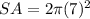
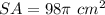
Find the surface area of the composite figure

`175\pi\ cm^(2)+98\pi\ cm^(2)=273\pi\ cm^(2)`