Question

MY NOTES

lim
n18
ASK YOUR TEACHER
Use the Limit Comparison Test to determine the convergence or divergence of the series.
00
n=1
n3
converges
O diverges
n+ 3
n+ 3
n3-5n+8
- 5n+ 8
Need Help?
-
=L>0
Read It
9,433
PRACTICE ANOTHER
Watch It
AUG
3
tv♫♬
(a
A

Answer 1

Answers:

Part 1)
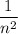`\displaystyle (1)/(n^2)` or 1/(n^2) goes in the box.

Part 2) The series converges

======================================================

Work Shown:

`\displaystyle L = \lim_(n\to \infty) (a_n)/(b_n)\\\\\\\displaystyle L = \lim_(n\to \infty) ((n+3)/(n^3-5n+8))/((1)/(n^2))\\\\\\\displaystyle L = \lim_(n\to \infty) (n+3)/(n^3-5n+8)*(n^2)/(1)\\\\\\\displaystyle L = \lim_(n\to \infty) (n^3+3n^2)/(n^3-5n+8)\\\\\\`

`\displaystyle L = \lim_(n\to \infty) ((n^3)/(n^3)+(3n^2)/(n^3))/((n^3)/(n^3)-(5n)/(n^3)+(8)/(n^3))\\\\\\\displaystyle L = \lim_(n\to \infty) (1+(3)/(n))/(1-(5)/(n^2)+(8)/(n^3))\\\\\\\displaystyle L = (1+0)/(1-0+0)\\\\\\\displaystyle L = 1\\\\\\`

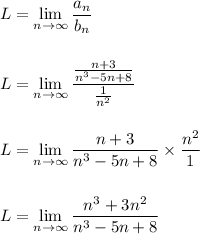
Because L is finite and positive, i.e.
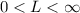`0 < L < \infty`, this means that the original series given and the series

`\displaystyle \sum_(n=1)^(\infty) (1)/(n^2)`

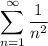
either converge together or diverge together due to the Limit Comparison Test.

But the simpler series is known to converge (p-series test).

Therefore, the original series converges as well.

The two series likely don't converge to the same value, but they both converge nonetheless.