Question

For 20 points! please help

Let z=13+7i and w=3(cos(1.43)+isin(1.43)
a. convert zw using De Moivre's theorem
b. calculate z/w using De Moivre's theorem

Answer 1

a)zw = 44.295 cos(1.924) +isin(1.924))

b) z/w= 4.921 cos(-0.936) + isin(-0.936)

Explanation:

Given:

z=13+7i

w=3(cos(1.43)+isin(1.43)

a. convert zw using De Moivre's theorem

First coverting z into polar form:

13^2 + 7^2 = 14.765

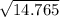`√(14.765)` =r

θ= arctan (7/13)

= 0.49394 (28.301 in degrees)

z= 14.765(cos(0.49394)+isin(0.49394) )

Now finding zw

zw= 14.765(cos(.494)+isin(.494))×3(cos(1.43)+isin(1.43))

Using De Moivre's theorem, the modulus will be multiplied

14.765 x 3=44.295

whereas the angles will be added

.494+1.43=1.924

Thus:

zw = 44.295 cos(1.924) +isin(1.924))

b)

finding z/w

z/w= 14.765(cos(.494)+isin(.494)) / 3(cos(1.43)+isin(1.43))

Using De Moivre's theorem, the modulus will be divided

14.765 / 3 = 4.921

whereas the angles will be subtracted:

.494-1.43=-0.936

Thus:

z/w= 4.921 cos(-0.936) + isin(-0.936) !