Answer:
The equation
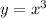 is not an equation of a simple , even polynomial function.
is not an equation of a simple , even polynomial function.
Explanation:
Even function : A function is even when its graph is symmetric with respect to y-axis.
Algebrically , the function f is even if and only if
f(-x)=f(x) for all x in the domain of f.
When the function does not satisfied the above condition then the function is called non even function.
f(x)
 f(-x)
f(-x)
Now , we check given function is even or not
A. y=
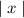
If x is replaced by -x
Then we get the function
f(-x)=
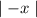
f(-x)=
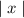
Hence, f(-x)=f(x)
Therefore , it is even polynomial function.
B.
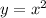
If x is replace by -x
Then we get
f(-x)=
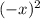
f(-x)=

Hence, f(-x)=f(x)
Therefore, it is even polynomial function.
C.
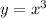
If x is replace by -x
Then we get
f(-x)=
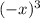
f(-x)=
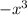
Hence, f(-x)
 f(x)
f(x)
Therefore, it is not even polynomial function.
D.
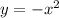
If x is replace by -x
Then we get
f(-x)= -
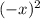
f(-x)=-

Hence, f(-x)=f(x)
Therefore, it is even polynomial function.
Answer: C.
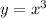 is not simple , even polynomial function.
is not simple , even polynomial function.