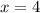Answer: Fourth Option
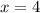
Explanation:
First we write the equation
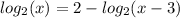
Now we use the properties of logarithms to simplify the expression

The property of the sum of logarithms says that:
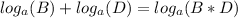
Then
![log_2[x(x-3)]= 2](https://img.qammunity.org/2020/formulas/mathematics/middle-school/qeeyrq3e0ngqmswjt9u4sl0azo6x0w1dhu.png)
Now use the property of the inverse of the logarithms
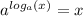
![2^(log_2[(x)(x-3)])= 2^2](https://img.qammunity.org/2020/formulas/mathematics/middle-school/862gog4bp35lpyufapquqm68fdm9uh7akz.png)
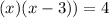
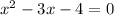
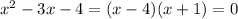
Then the solution are
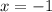 and
and

We take the positive solution because the logarithm of a negative number does not exist
Finally the solution is: