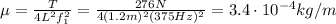Question

A string attached to an oscillator at one end forms 5 nodes (counting the two ends) and produces a frequency of ν = 1.5 kHz. The string is L = 1.2 m long and is under a tension of T = 276 N.

What is the linear density of the string, in kilograms per meter?

Answer 1

`3.4\cdot 10^(-4) kg/m`

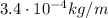
Step-by-step explanation:

The order of the harmonics for standing waves in a string is equal to the number of nodes minus 1, so

n = 5 - 1 = 4

In this case, the frequency of the 4th-harmonic is

`f_4=1.5 kHz = 1500 Hz`

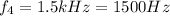
We also know the relationship between the frequency of the nth-harmonic and the fundamental frequency:

`f_4 = 4 f_1`

so we find the fundamental frequency:

`f_1 = (f_4)/(4)=(1500 Hz)/(4)=375 Hz`

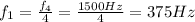
The fundamental frequency is given by

`f_1 = (1)/(2L)\sqrt{(T)/(\mu)}`

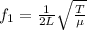
where

L = 1.2 m is the length of the string

T = 276 N is the tension in the string

`\mu` is the linear density

Solving the equation for
`\mu`, we find

`\mu = (T)/(4L^2 f_1^2)=(276 N)/(4(1.2 m)^2(375 Hz)^2)=3.4\cdot 10^(-4) kg/m`