Answer:
A) x=5 or -11
Explanation:
The given equation is:
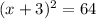
The most suitable method so solve this quadratic equation is the square root method.
We take square root of both sides to obtain:
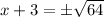
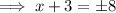

We now split the plus or minus sign to get;
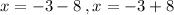
This simplifies to:
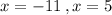
The correct choice is A