Question

The difference between the roots of the equation 2x^2−5x+c=0 is 0.25. Find c.

Answer 1

The value of c is 3.09375.

Explanation:

Given : The difference between the roots of the equation
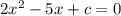`2x^2-5x+c=0` is 0.25.

To find : The value of c?

Solution :

The general quadratic equation is
`ax^2+bx+c=0` with roots
`\alpha,\beta`

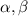
The sum of roots is
`\alpha+\beta=-(b)/(a)`

The product of roots is
`\alpha\beta=(c)/(a)`

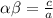
On comparing with given equation, a=2, b=-5 and c=c

Substitute the values,

The sum of roots is
`\alpha+\beta=-(-5)/(2)`

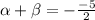
`\alpha+\beta=(5)/(2)` .....(1)

The product of roots is
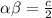`\alpha\beta=(c)/(2)` ....(2)

The difference between roots are
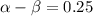`\alpha-\beta=0.25` .....(3)

Using identity,

`\alpha-\beta=√((\alpha+\beta)^2-4\alpha\beta)`

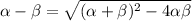
Substitute the value in the identity,

`0.25=\sqrt{((5)/(2))^2-4((c)/(2))}`

`0.25=\sqrt{(25)/(4)-2c}`

`0.25=\sqrt{(25-8c)/(4)}`

`0.25* 2=√(25-8c)`

`0.5=√(25-8c)`

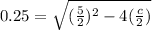
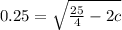
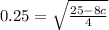
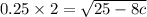
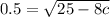
Squaring both side,

`0.5^2=25-8c`

`0.25=25-8c`

`8c=25-0.25`

`8c=24.75`

`c=(24.75)/(8)`

`c=3.09375`

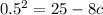
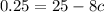
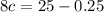
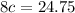
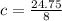
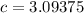
Therefore, the value of c is 3.09375.

Answer 2

`c=(99)/(32)`

Explanation:

The given quadratic equation is
`2x^2-5x+c=0`.

Comparing this equation to:
`ax^2+bx+c=0`, we have a=2,b=-5.

Where:
`x_1+x_2=(5)/(2)` and
`x_1x_2=(c)/(2)`

The difference in roots is given by:

`x_2-x_1=√((x_1+x_2)^2-4x_1x_2)`

`\implies 0.25=\sqrt{(2.5)^2-4((c)/(2))}`

`\implies 0.25^2=6.25-2c`

`\implies 0.0625-6.25=-2c`

`\implies -6.1875=-2c`

Divide both sides by -2

`c=(99)/(32)`