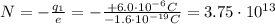Question

A small cork with an excess charge of +6.0µC is placed 0.12 m from another cork, which carries a charge of -4.3µC.

A) what is the magnitude of the eletric force between the corks?
B) is this force attractive or repulsive?
C) how many excess electrons are on the negative cork?
D) how many electrons has the postive cork lost?

Answer 1

A) 16.1 N

The magnitude of the electric force between the corks is given by Coulomb's law:

`F=k(q_1 q_2)/(r^2)`

where

k is the Coulomb's constant

`q_1 = 6.0 \mu C=6.0 \cdot 10^(-6) C` is the magnitude of the charge on the first cork

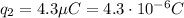`q_2 = 4.3 \mu C = 4.3 \cdot 10^(-6)C` is the magnitude of the charge of the second cork

r = 0.12 m is the separation between the two corks

Substituting numbers into the formula, we find

`F=(9\cdot 10^9 N m^2 C^(-2) )((6.0\cdot 10^(-6)C)(4.3\cdot 10^(-6) C))/((0.12 m)^2)=16.1 N`

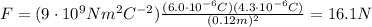
B) Attractive

According to Coulomb's law, the direction of the electric force between two charged objects depends on the sign of the charge of the two objects.

In particular, we have:

- if the two objects have charges with same sign (e.g. positive-positive or negative-negative), the force is repulsive

- if the two objects have charges with opposite sign (e.g. positive-negative), the force is attractive

In this problem, we have

Cork 1 has a positive charge

Cork 2 has a negative charge

So, the force between them is attractive.

C)
`2.69\cdot 10^(13)`

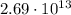
The net charge of the negative cork is

`q_2 = -4.3 \cdot 10^(-6)C`

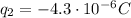
We know that the charge of a single electron is

`e=-1.6\cdot 10^(-19)C`

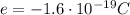
The net charge on the negative cork is due to the presence of N excess electrons, so we can write

`q_2 = Ne`

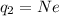
and solving for N, we find the number of excess electrons:

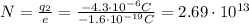
`N=(q_2)/(e)=(-4.3\cdot 10^(-6) C)/(-1.6\cdot 10^(-19) C)=2.69\cdot 10^(13)`

D)
`3.75\cdot 10^(13)`

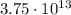
The net charge on the positive cork is

`q_1 = +6.0\cdot 10^(-6)C`

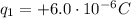
We know that the charge of a single electron is

`e=-1.6\cdot 10^(-19)C`

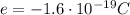
The net charge on the positive cork is due to the "absence" of N excess electrons, so we can write

`q_1 = -Ne`

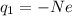
and solving for N, we find the number of electrons lost by the cork:

`N=-(q_1)/(e)=-(+6.0\cdot 10^(-6) C)/(-1.6\cdot 10^(-19) C)=3.75\cdot 10^(13)`