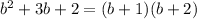You can factor a polynomial by finding its roots: if
 is a solution of
is a solution of
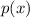 , i.e.
, i.e.
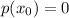 , then
, then
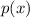 is divisible by
is divisible by
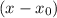 .
.
You keep factoring the polynomial until the remaining factor has no more roots, and is thus irreducible.
In this case, we have
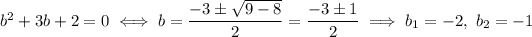
So, the polynomial can be written as