Question

The graph of this system of equations is used to solve 4x2-3+6=2x4-9x3+2x What represents the solution set?

y intercepts of the graph

x intercepts of the graph

y coordinates of the intersection points

x coordinates of the intersection points

Answer 1

Answer: It's D

Explanation:

Answer 2

x coordinates of the intersection points

EXPLANATION

The given system of equations is:

`y = 4 {x}^(2) - 3x + 6`

`y = 2 {x}^(4) - 9 {x}^(3) + 2x`

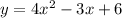
We want to use the graph of these functions to solve

`4 {x}^(2) - 3x + 6 = 2 {x}^(4) - 9 {x}^(3) + 2x`

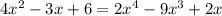
The point of the intersection of the graph gives the solution to the simultaneous equation above.

Hence the x-coordinates of the intersection points gives the solution set of

`4 {x}^(2) - 3x + 6 = 2 {x}^(4) - 9 {x}^(3) + 2x`

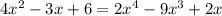
The last choice is correct.