Question

Three disks are spinning independently on the same axle without friction. Their respective rotational inertias and angular speeds are I,ω (clockwise); 2I,3ω (counterclockwise); and 4I,ω/2 (clockwise). The disks then slide together and stick together, forming one piece with a single angular velocity. What will be the direction and the rate of rotation ωnet of the single piece? Express your answer in terms of one or both of the variables I and ω and appropriate constants. Use a minus sign for clockwise rotation.

Answer 1

3/7 ω

Step-by-step explanation:

Initial momentum = final momentum

I(-ω) + (2I)(3ω) + (4I)(-ω/2) = (I + 2I + 4I) ωnet

-Iω + 6Iω - 2Iω = 7I ωnet

3Iω = 7I ωnet

ωnet = 3/7 ω

The final angular velocity will be 3/7 ω counterclockwise.

Answer 2

`\omega_(net) = 3\omega/7`

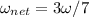
Step-by-step explanation:

For this problem we will use the conservation of angular momentum. This is, the momenta of each disk added together is equal to the momenta of the single piece at angular velocity
`\omega_(net)`. If

`L_(0) = -I\omega-4I(\omega)/(2)+2I(3\omega) \\L_(0) = -I\omega-2I\omega+6I\omega \\L_(0) = 3I\omega\\`,

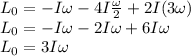and because all disks are spinning on the same axle, the total inertia moment of the single piece at angular velocity
`\omega_(net)` is the sum of the inertia moment of the three disks. This way, we have that

`L_(f) = (I+2I+4I)\omega_(net)\\\\L_(f)=7I\omega_(net)\\`.

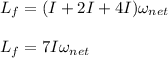The conservation of angular momentum leads us to

`L_(0)=L_(f)\\`,

`3I\omega = 7I\omega_(net)\\`,

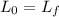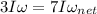thus

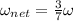`\omega_(net) = (3)/(7)\omega`.