Answer:
w = -11
Explanation:
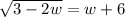
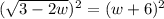
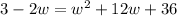
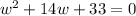
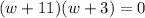
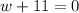 or
or
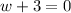
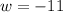 or
or
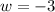
When you square both sides of an equation, you must check all solutions for extraneous solutions.
Check w = -11.
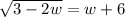
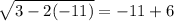
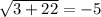
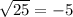
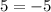
This is a false statement, so the solution w = -11 is extraneous since it does not satisfy the original equation.
Check w = -3.
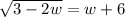
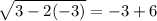
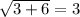
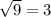
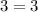
This is a true statement, so the solution w = -3 is valid.
Answer: w = -11