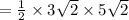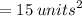Question

Find the area of the quadrilateral QRST by using the formula for the area of a kite. HELP PLEASE!!!!

A. 15 units^2
B. 10 units ^2
C. 16 units ^2
D. 5 units ^2

Answer 1

A. 15 units^2

Step-by-step explanation

The area of kite is half the product of the diagonals.

The first diagonal has vertices at,

T(0,0) and R(5,5).

The length of this diagonal is

`TR = \sqrt{ {5}^(2) + {5}^(2) }`

`TR = √(25 + 25)`

`TR = √(50) =5 √(2)`

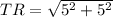
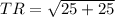
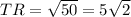
The other diagonal has vertices at;

Q(0,3) and S(3,0).

The length of this diagonal is

`QS = \sqrt{ {3}^(2) + {3}^(2) }`

`QS = √( 9+ 9 )`

`QS = √(18) = 3 √(2)`

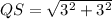
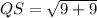
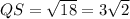
The area of the kite is

`= (1)/(2) * 3 √(2) * 5 √(2)`

`= 15 \: {units}^(2)`