Answer:
The required expression is
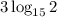 .
.
Explanation:
According to the power property of exponent,
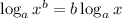
The given expression is
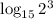
Here a=15, x=2, b=3.
Using power property of exponent the given expression can be written as
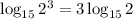
Therefore the required expression is
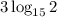 .
.